This famous (Fisher’s or Anderson’s) iris data set gives the measurements in centimeters of the variables sepal length and width and petal length and width, respectively, for 50 flowers from each of 3 species of iris. The species are Iris setosa, versicolor, and virginica.

###################################################
### use iris dataset to test classify models
###################################################

# load the data set
data(iris)

#########################
# explore the data set
#########################

head(iris)
##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa
str(iris)
## 'data.frame':    150 obs. of  5 variables:
##  $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
##  $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
##  $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
##  $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
summary(iris)
##   Sepal.Length    Sepal.Width     Petal.Length    Petal.Width          Species  
##  Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100   setosa    :50  
##  1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300   versicolor:50  
##  Median :5.800   Median :3.000   Median :4.350   Median :1.300   virginica :50  
##  Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199                  
##  3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800                  
##  Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500

Let us see some relationships between variables in the iris data set.

#  visualizing relationships between variables
library(ggplot2)
ggplot(iris, aes(x = Sepal.Length, y = Sepal.Width, col = Species, shape = Species)) +
  geom_point()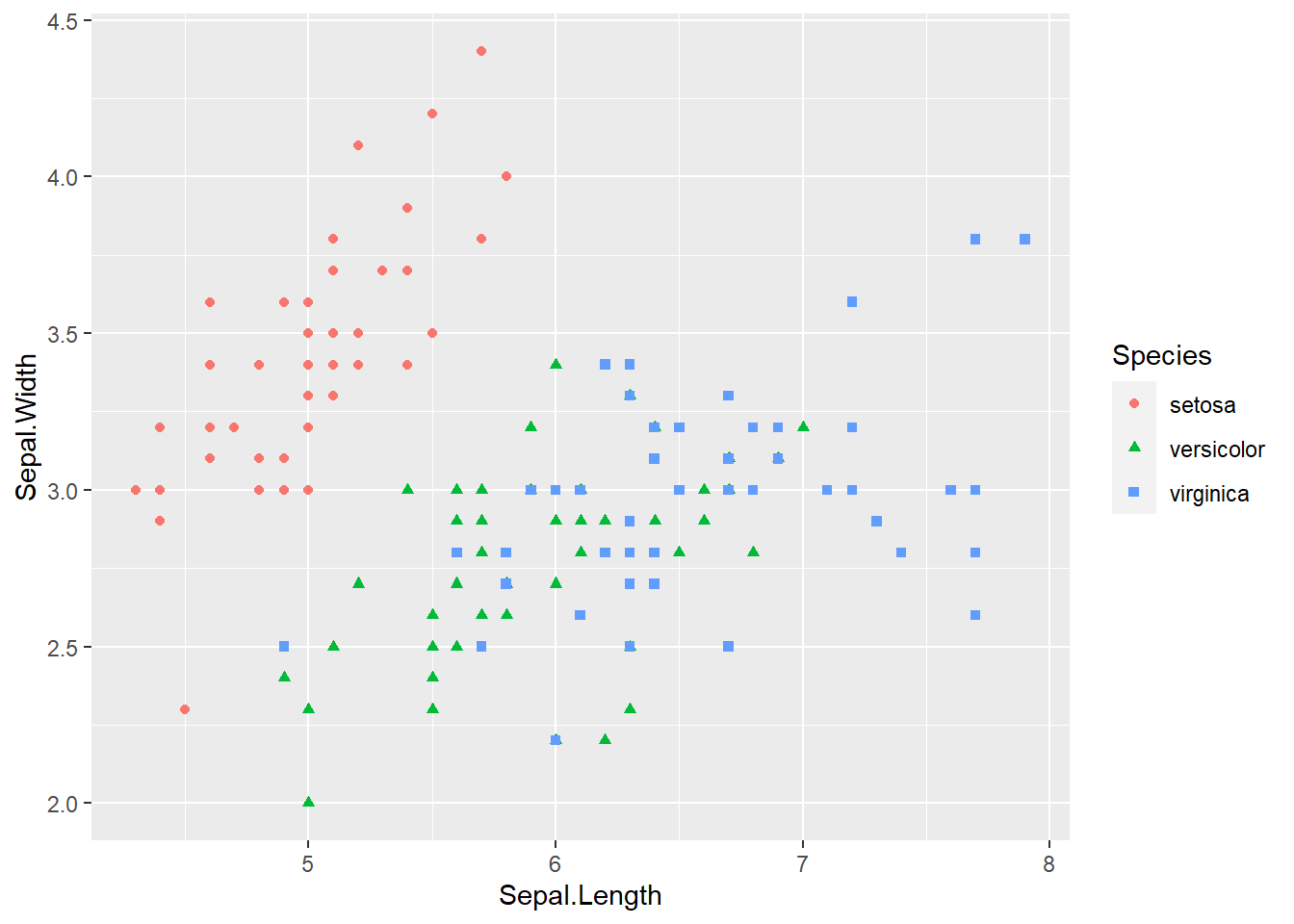

ggplot(iris, aes(x = Sepal.Length, y = Petal.Length, col = Species, shape = Species)) +
  geom_point()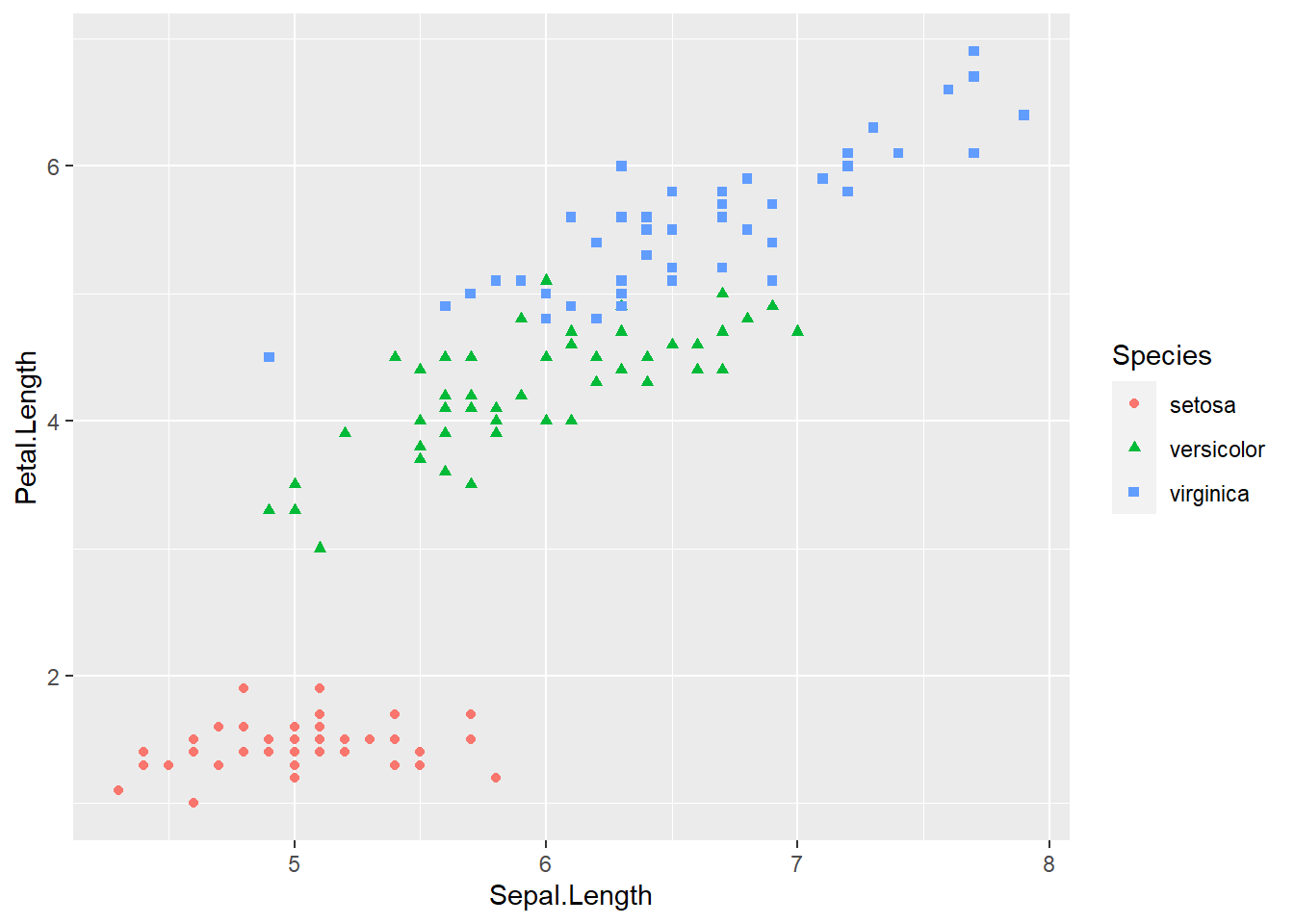

ggplot(iris, aes(x = Sepal.Length, y = Petal.Width, col = Species, shape = Species)) +
  geom_point()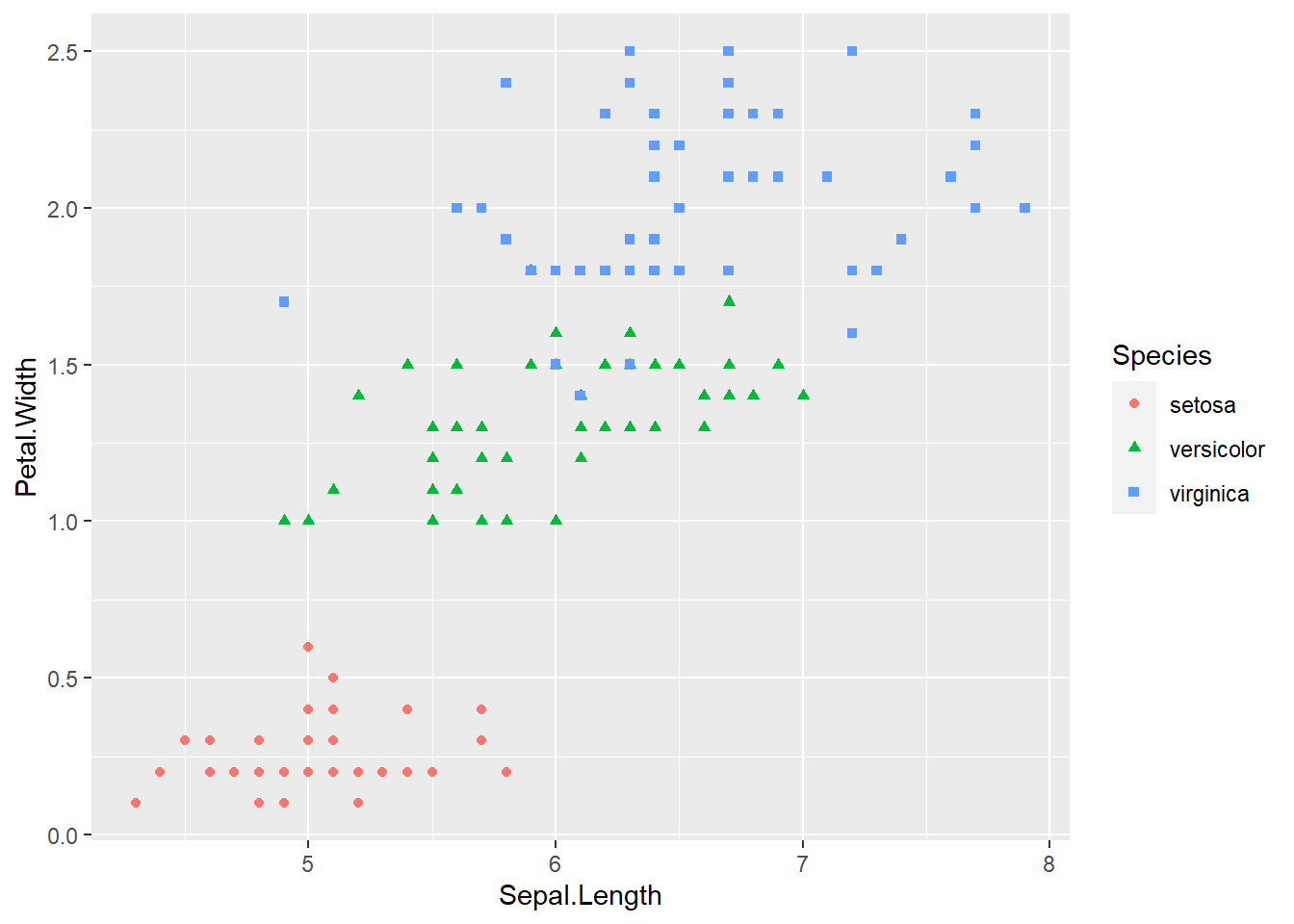

ggplot(iris, aes(x = Sepal.Width, y = Petal.Length, col = Species, shape = Species)) +
  geom_point()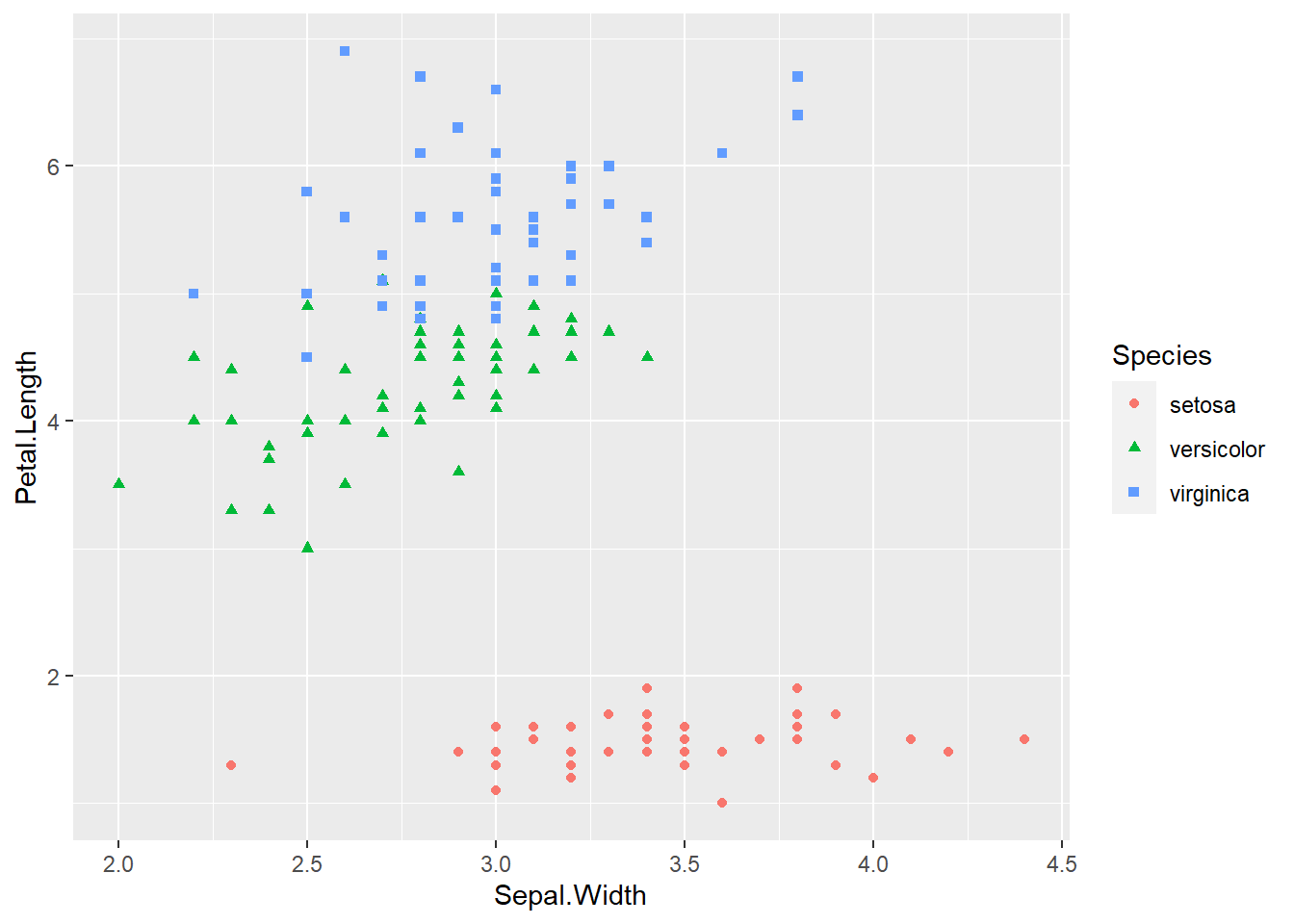

ggplot(iris, aes(x = Sepal.Width, y = Petal.Width, col = Species, shape = Species)) +
  geom_point()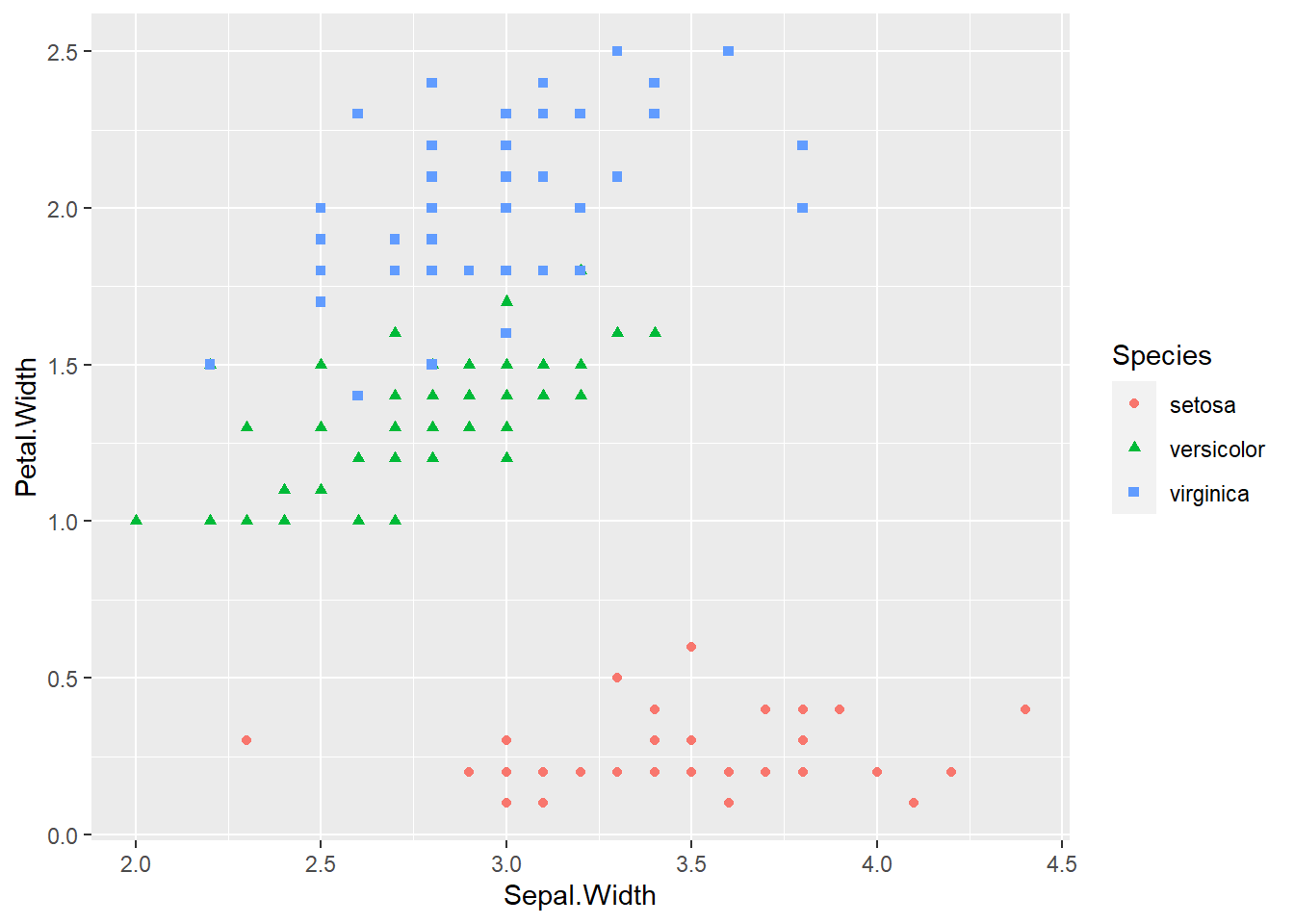

ggplot(iris, aes(x = Petal.Width, y = Petal.Length, col = Species, shape = Species)) +
  geom_point()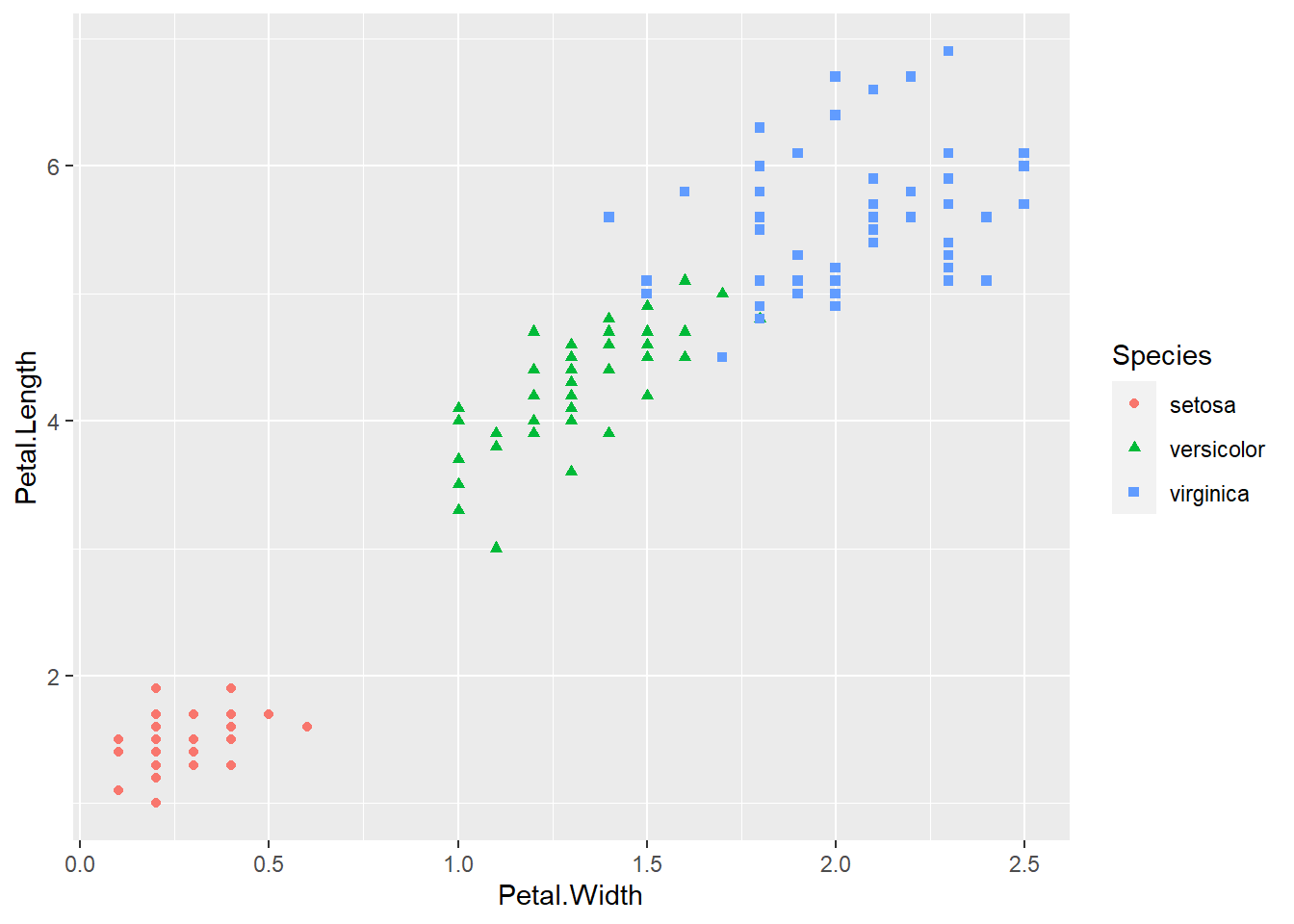

The species of setosa is easy identify by petal width or petal length, the other species are somewhat difficult to classify.

Then we split iris data set to train-set and test-set.

#########################################
##  split the data set to train and test
#########################################

n <- length(iris[,1])
index1 <- 1 : n
# divide to 5 part of data
index2 <- rep(1 : 5, ceiling(n / 5))[1 : n]
set.seed(100)
# melt the order of the data
index2 <- sample(index2, n)
# get the one part of the data
m <- index1[index2 == 1]
trainset <- iris[-m, ]
testset <- iris[m, ]
str(trainset)
## 'data.frame':    120 obs. of  5 variables:
##  $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
##  $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
##  $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
##  $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...

Let us try to do some classification models.

Logistic regression is mainly for 2 response classes, and for linear decision boundaries.Of course, we could also classify the species of setosa first, then use logic regression to classify the other species, but we did not try it in here.

Discriminant analysis is popular for multiple-class classification.Here, we assume the decision boundary is linear, so we use linear discriminant analysis model.

#####################################
## try kinds of classify models
#####################################

## linear discriminant analysis
library(MASS)
lda_model <- lda(Species ~ ., data = trainset)
lda_model
## Call:
## lda(Species ~ ., data = trainset)
## 
## Prior probabilities of groups:
##     setosa versicolor  virginica 
##  0.3333333  0.3333333  0.3333333 
## 
## Group means:
##            Sepal.Length Sepal.Width Petal.Length Petal.Width
## setosa           4.9700      3.3975       1.4625      0.2425
## versicolor       5.9075      2.7525       4.2450      1.3150
## virginica        6.6300      2.9975       5.5900      2.0400
## 
## Coefficients of linear discriminants:
##                     LD1         LD2
## Sepal.Length  0.6090357  0.06544054
## Sepal.Width   1.4196508  2.20984856
## Petal.Length -2.0519675 -0.91661473
## Petal.Width  -2.8551780  2.70280342
## 
## Proportion of trace:
##    LD1    LD2 
## 0.9896 0.0104
plot(lda_model)

lda_pred <- predict(lda_model, testset)

Let us see the confusion matrix and accurate from linear discriminant analysis model.

table(lda_pred$class, testset$Species)
##             
##              setosa versicolor virginica
##   setosa         10          0         0
##   versicolor      0         10         1
##   virginica       0          0         9
mean(lda_pred$class == testset$Species)
## [1] 0.9666667

K-nearest neighbor model is mainly for complicated decision boundary, and for few features.If there are much many features, this model will dive into the curse of dimension.

In this model, the scale of the variables matters, because this classifier predicts the class of a given test observation by identifying distance, so to standardize the data is a good way.

## k-nearest neighbor
library(class)
train_x <- as.matrix(trainset[, 1:4])
test_x <- as.matrix(testset[, 1:4])
train_y <- trainset[, 5]

set.seed(1)
knn_pred <- knn(train_x, test_x, train_y, k = 1)

table(knn_pred, testset$Species)
##             
## knn_pred     setosa versicolor virginica
##   setosa         10          0         0
##   versicolor      0         10         2
##   virginica       0          0         8
mean(knn_pred == testset$Species)
## [1] 0.9333333

Decision tree is a classic model. It is simple and easy to explain to people.However, trees generally do not have high accuracy.

## decision tree
library(tree)
## Registered S3 method overwritten by 'tree':
##   method     from
##   print.tree cli
tree_model <- tree(Species ~ ., trainset)
summary(tree_model)
## 
## Classification tree:
## tree(formula = Species ~ ., data = trainset)
## Variables actually used in tree construction:
## [1] "Petal.Length" "Petal.Width"  "Sepal.Length"
## Number of terminal nodes:  5 
## Residual mean deviance:  0.1813 = 20.85 / 115 
## Misclassification error rate: 0.03333 = 4 / 120

Decision tree can be displayed graphically.

plot(tree_model)
text(tree_model, pretty = 0)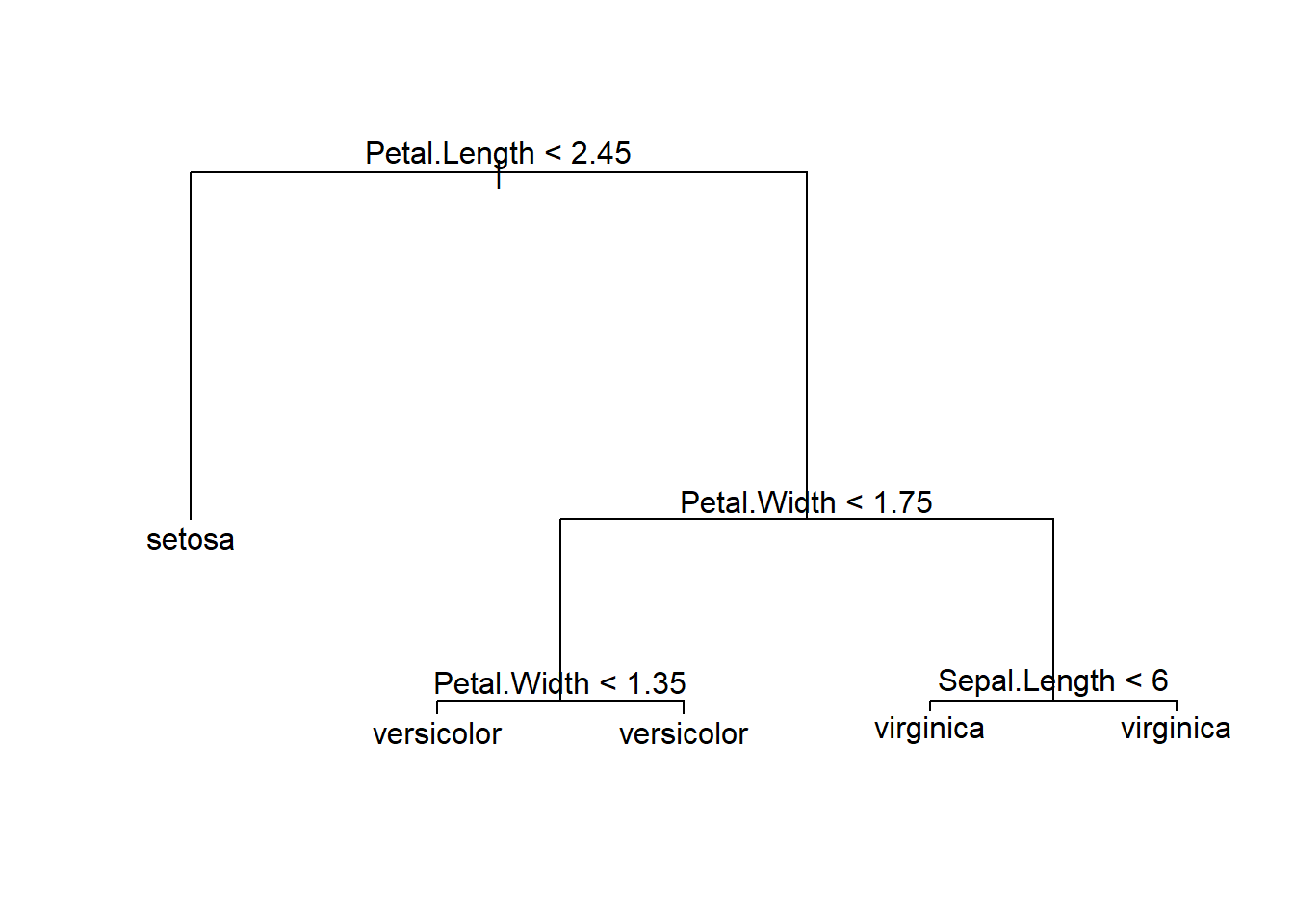

The confusion matrix and accuracy from decision tree model.

tree_pred <- predict(tree_model, testset, type = "class")

table(tree_pred, testset$Species)
##             
## tree_pred    setosa versicolor virginica
##   setosa         10          0         0
##   versicolor      0         10         2
##   virginica       0          0         8
mean(tree_pred == testset$Species)
## [1] 0.9333333

By aggregating many decision trees, using models like bagging, random forests, and boosting, the accuracy of tree can be substantially improved.

## bagging
library(randomForest)
## randomForest 4.6-14
## Type rfNews() to see new features/changes/bug fixes.
## 
## 载入程辑包：'randomForest'
## The following object is masked from 'package:ggplot2':
## 
##     margin
bag_model <- randomForest(Species ~ ., data = trainset, mtry = 4,
                          importance = TRUE)
bag_model
## 
## Call:
##  randomForest(formula = Species ~ ., data = trainset, mtry = 4,      importance = TRUE) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 4
## 
##         OOB estimate of  error rate: 4.17%
## Confusion matrix:
##            setosa versicolor virginica class.error
## setosa         40          0         0       0.000
## versicolor      0         37         3       0.075
## virginica       0          2        38       0.050
bag_pred <- predict(bag_model, newdata = testset)
plot(bag_pred, testset$Species)

table(bag_pred, testset$Species)
##             
## bag_pred     setosa versicolor virginica
##   setosa         10          0         0
##   versicolor      0         10         2
##   virginica       0          0         8
mean(bag_pred == testset$Species)
## [1] 0.9333333

The main difference between bagging and random forests is the choice of predictor subset size.

##  random forestlibrary(randomForest)
rf_model <- randomForest(Species ~ ., data = trainset, 
                          importance = TRUE)
rf_model
## 
## Call:
##  randomForest(formula = Species ~ ., data = trainset, importance = TRUE) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 2
## 
##         OOB estimate of  error rate: 5%
## Confusion matrix:
##            setosa versicolor virginica class.error
## setosa         40          0         0       0.000
## versicolor      0         37         3       0.075
## virginica       0          3        37       0.075

Random forest could also supply us the importance of variables.

rf_pred <- predict(rf_model, newdata = testset)
plot(rf_pred, testset$Species)

importance(rf_model)
##                 setosa versicolor virginica MeanDecreaseAccuracy MeanDecreaseGini
## Sepal.Length  7.613543   6.818930  9.557335            11.838471         9.273543
## Sepal.Width   5.531353   2.260127  3.547368             5.997058         2.151328
## Petal.Length 23.581406  29.663793 26.582862            33.405993        33.149589
## Petal.Width  20.999556  27.430154 34.330308            33.420164        34.668673
varImpPlot(rf_model)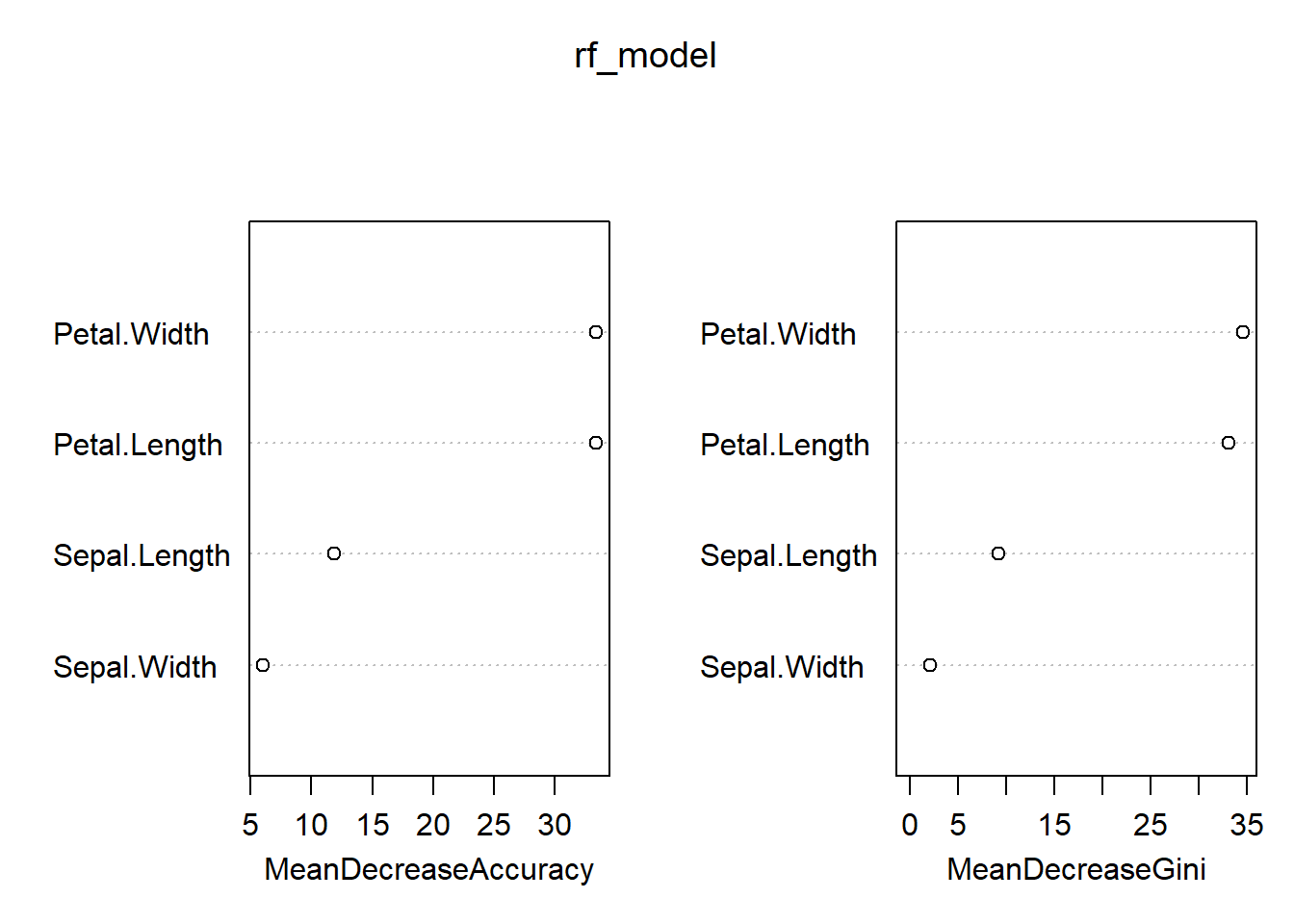

table(rf_pred, testset$Species)
##             
## rf_pred      setosa versicolor virginica
##   setosa         10          0         0
##   versicolor      0         10         2
##   virginica       0          0         8
mean(rf_pred == testset$Species)
## [1] 0.9333333

In boosting, because the growth of a particular tree takes into account the other trees that have already been grown, smaller trees are typically sufficient.

## boosting
library(gbm)
## Loaded gbm 2.1.8
boost_model <- gbm(Species ~ ., data = trainset)
## Distribution not specified, assuming multinomial ...
## Warning: Setting `distribution = "multinomial"` is ill-advised as it is currently broken. It exists
## only for backwards compatibility. Use at your own risk.
summary(boost_model)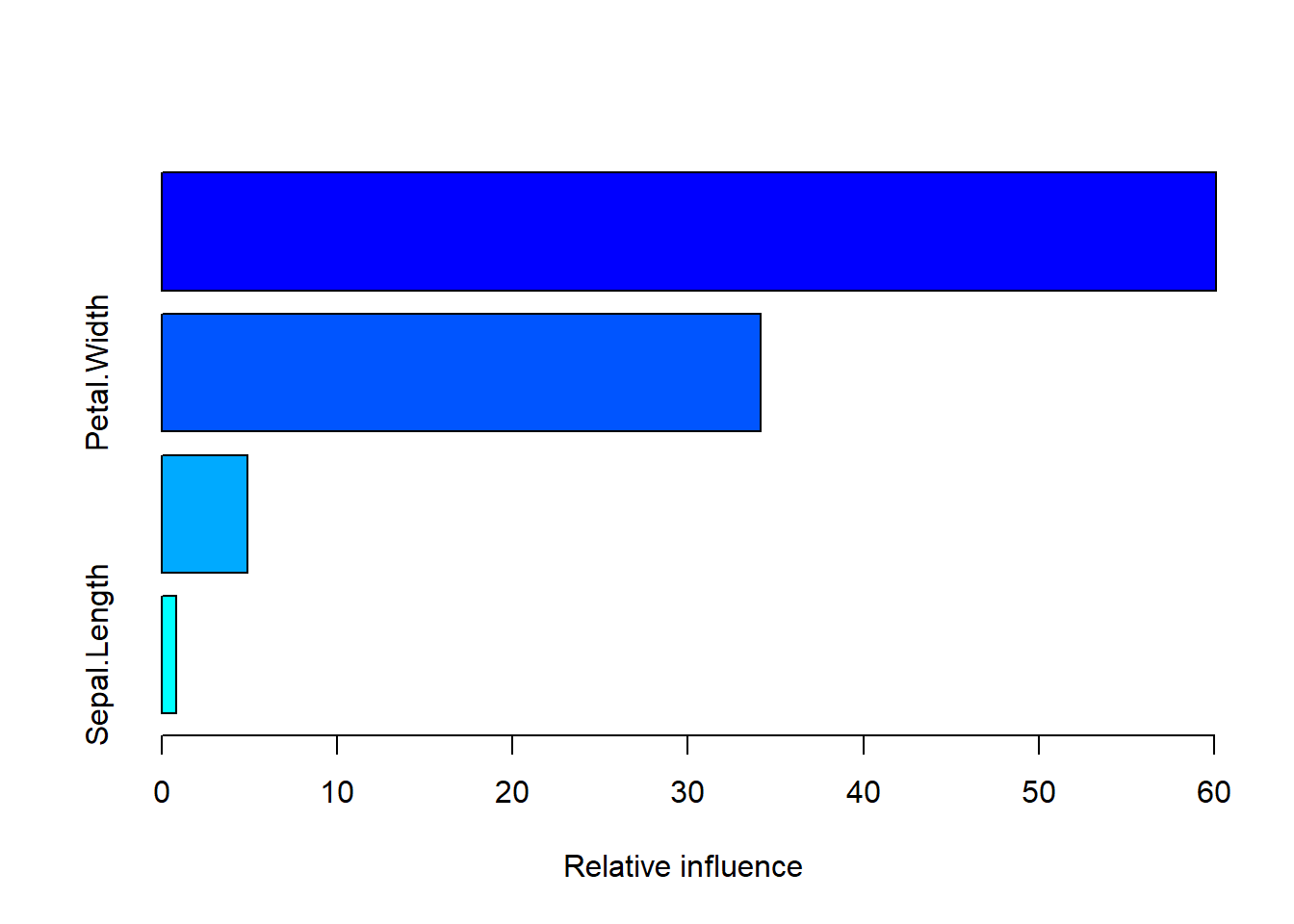

##                       var    rel.inf
## Petal.Length Petal.Length 60.1021627
## Petal.Width   Petal.Width 34.1425780
## Sepal.Width   Sepal.Width  4.9146578
## Sepal.Length Sepal.Length  0.8406015
boost_pred <- predict(boost_model, newdata = testset, n.trees = 100,
                      type = "response")

temp = data.frame(boost_pred[, , 1])
temp2 = apply(temp, 1, which.max)
boost_pred2 <- names(temp)[temp2]

table(boost_pred2, testset$Species)
##             
## boost_pred2  setosa versicolor virginica
##   setosa         10          0         0
##   versicolor      0         10         2
##   virginica       0          0         8
mean(boost_pred2 == testset$Species)
## [1] 0.9333333

Support vector machine model:

##  support vector machine
library(e1071)
svm_model <- svm(Species ~ ., data = trainset,
                 kernel = "linear", scale = FALSE)
summary(svm_model)
## 
## Call:
## svm(formula = Species ~ ., data = trainset, kernel = "linear", scale = FALSE)
## 
## 
## Parameters:
##    SVM-Type:  C-classification 
##  SVM-Kernel:  linear 
##        cost:  1 
## 
## Number of Support Vectors:  23
## 
##  ( 3 11 9 )
## 
## 
## Number of Classes:  3 
## 
## Levels: 
##  setosa versicolor virginica
svm_pred <- predict(svm_model, testset)

table(svm_pred, testset$Species)
##             
## svm_pred     setosa versicolor virginica
##   setosa         10          0         0
##   versicolor      0         10         0
##   virginica       0          0        10
mean(svm_pred == testset$Species)
## [1] 1

Naive bayes model:

## naive bayes
library(e1071)
bayes_model <- naiveBayes(trainset[, 1:4], trainset$Species)
summary(bayes_model)
##           Length Class  Mode     
## apriori   3      table  numeric  
## tables    4      -none- list     
## levels    3      -none- character
## isnumeric 4      -none- logical  
## call      3      -none- call
bayes_pred <- predict(bayes_model, testset[, 1:4], type = "class")

table(bayes_pred, testset$Species)
##             
## bayes_pred   setosa versicolor virginica
##   setosa         10          0         0
##   versicolor      0          9         2
##   virginica       0          1         8
mean(bayes_pred == testset$Species)
## [1] 0.9

Artificial neural networks model:

## artificial neural networks
library(nnet)
ann_model <- nnet(Species ~ ., data = trainset, size = 3)
## # weights:  27
## initial  value 131.269030 
## iter  10 value 55.781204
## iter  20 value 55.461173
## iter  30 value 55.453487
## iter  40 value 55.414230
## iter  50 value 48.507540
## iter  60 value 12.162402
## iter  70 value 4.001708
## iter  80 value 1.190122
## iter  90 value 0.029758
## iter 100 value 0.000278
## final  value 0.000278 
## stopped after 100 iterations
ann_pred <- predict(ann_model, newdata = testset, type = "class")

table(ann_pred, testset$Species)
##             
## ann_pred     setosa versicolor virginica
##   setosa         10          0         0
##   versicolor      0         10         3
##   virginica       0          0         7
mean(ann_pred == testset$Species)
## [1] 0.9

There are three models achieved highest correct rate 0.9666667.

They are linear discriminant analysis, support vector machine and artificial neural net.

Referenced books:

  1. Machine Learning with R

  2. Applied Predictive Modeling

  3. An Introduction to Statistical Learning with Applications in R

Just record, this article was posted at linkedin, and have 238 views to November 2021.