重讀《An introduction to statistical learning》筆記 第四章
2015-05-24
chapter 4 Classification
- 3 methods :
- logistic regression
- linear discriminant analysis
- K - nearest neighbors
- other computer-intensive methods
- generalized additive models
- trees
- random forests
- boosting
- support vector machine
- logistic regression
邏輯回歸對Y屬於某個分類的概率進行建模。
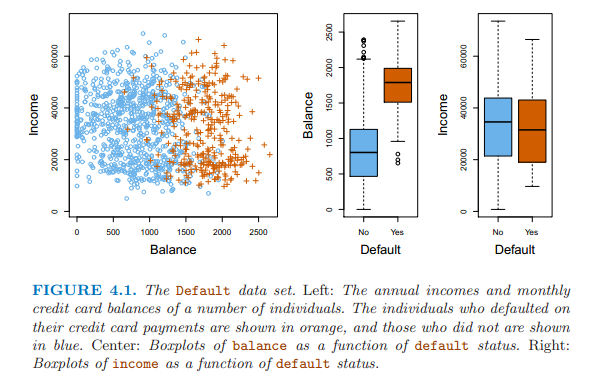
下面是示例用數據集,Y變量:是否拖欠債務;解釋變量是income和balance。
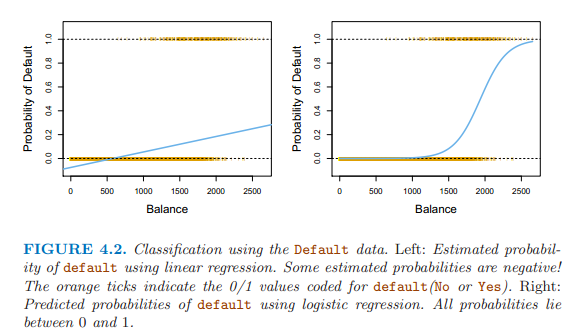
下圖左邊是使用線性回歸對Y變量分析,概率有負值,右邊是邏輯回歸進行建模,概率在0和1之間。
線性回歸的形式對Y屬於某類別的概率進行建模 \[p(X) = \beta_0 + \beta_1X\]
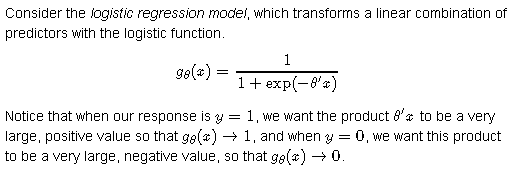
使用邏輯斯形式,把概率值規範在0和1之間 \[p(X) = \frac{e^{\beta_0 + \beta_1X}}{1+e^{\beta_0 + \beta_1X}}\]
方程變換后的模型: \[\frac{p(X)}{1 - p(X)} = e^{\beta_0 + \beta_1X}\]
方程左邊是個比值,數值偏向兩端。
優勢比,出現正面的概率比上出現反面的概率的比值,
如0.2/(1-0.2)=0.25
0.9/(1-0.9)=9
爲了讓比值平穩,對方程兩邊同時取對數,得到: \[log(\frac{p(X)}{1-p(X)}) = \beta_0 + \beta_1X\]
估計回歸係數:最大似然法 maximum likelihood選擇能夠最大化下面的似然方程的係數值。
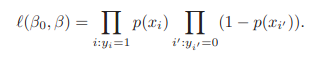
最小平方法是最大似然法的特例。
最大似然法常用於擬合非線性模型。
邏輯斯回歸中也可以使用離散變量做解釋變量,使用虛擬變量的形式。
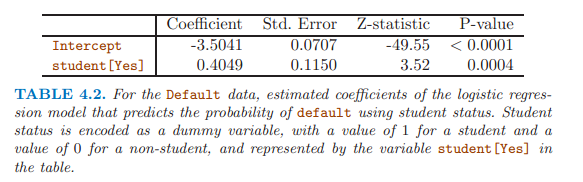
在單變量邏輯回歸中,離散變量學生顯著,而且係數為正,表明學生容易拖欠信用卡。
多變量邏輯回歸 \[log(\frac{p(X)}{1-p(X)}) = \beta_0 + \beta_1X_1 + ... + \beta_pX_p\]
\[p(X) = \frac{e^{\beta_0 + \beta_1X_1 + ... + \beta_pX_p}}{1+e^{\beta_0 + \beta_1X_1 + ... + \beta_pX_p}}\]
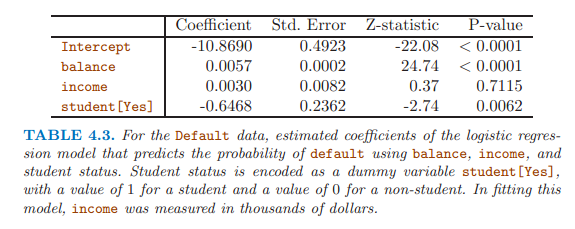
在多變量邏輯回歸中,離散變量學生顯著,係數為負,表明學生不易拖欠信用卡,與單變量邏輯回歸的結果剛好相反。
單變量回歸時考慮的是下圖左圖中的虛線,學生和非學生的整體拖欠水平,學生較高;
多變量中考慮的是下圖左圖中的實線,同樣的balance值,非學生的拖欠更高。
原因在于:學生因素和變量balance相關。
因此,單變量回歸很危險,當單變量可能與其他變量相關時。

- linear discriminant analysis
使用于當Y變量有三個以上類別
使用貝葉斯理論分類 \[Pr(Y=k|X =x) = \frac{\pi_kf_k(x)}{\sum_{l=1}^K\pi_lf_l(x)}\]
lda for p = 1
假定對於某個觀察值屬於第k個類別的解釋變量的密度函數是正態分佈或高斯分佈,分佈如下所示: \[f_k(x) = \frac{1}{\sqrt{2\pi}\sigma_k}exp(-\frac{1}{2\sigma_k^2}(x-\mu_k)^2)\]
插入計算后驗概率的公式得到: \[p_k(x) = \frac{\pi_k\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{1}{2\sigma^2}(x-\mu_k)^2)}{\sum_{l=1}^K\pi_l\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{1}{2\sigma^2}(x-\mu_l)^2)}\]
$\pi_k$代表一個隨機選擇的觀察值屬於第k類別的先驗概率。
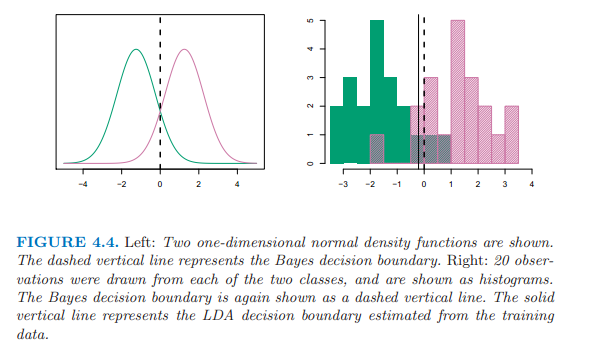
LDA近似貝葉斯分類器,通過插入一些係數估計值, \[\hat{\mu_k} = \frac{1}{n_k}\sum_{i:y_i=k}x_i\]
\[\hat{\sigma}^2 = \frac{1}{n-K}\sum_{k=1}^K\sum_{i:y_i=k}(x_i - \hat{\mu}_k)^2\]
\[\hat{\pi}_k = n_k/n\]
加入計算后驗概率的公式,兩遍取對數,適當變換,得到discriminant functions, 他是x的線性方程。
\[\hat{\delta}_k(x) = x \cdot \frac{\hat{\mu}_k}{\hat{\sigma}^2} - \frac{\hat{\mu}_k^2}{2\hat{\sigma}^2} + log(\hat{\pi}_k)\]
lda for p > 1
假定解釋變量服從多變量高斯分佈,有均值和共同的協方差矩陣。
\[f(x) = \frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))\]
求和符號代表協方差矩陣。
\[\delta_k(x) = x^T\Sigma^{-1}\mu_k-\frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k + log\pi_k\]

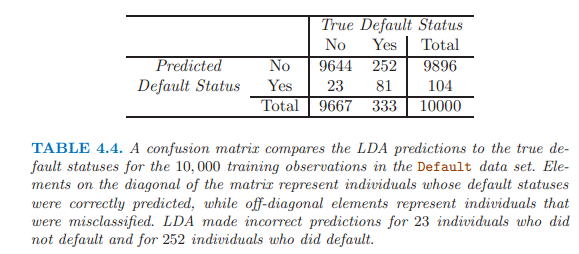
LDA嘗試近似貝葉斯分類器,取得最小的總體錯誤率。
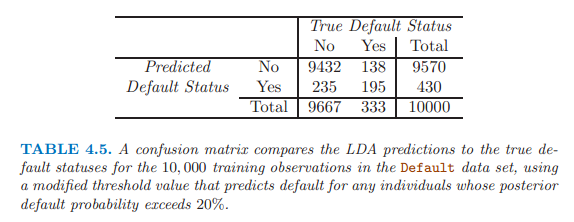
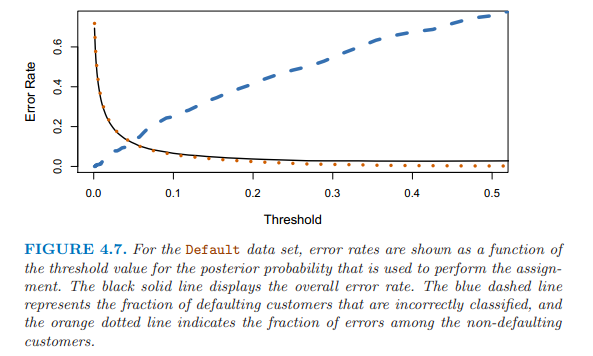
貝葉斯分類器使用臨界值0.5,有最小的總體錯誤率。
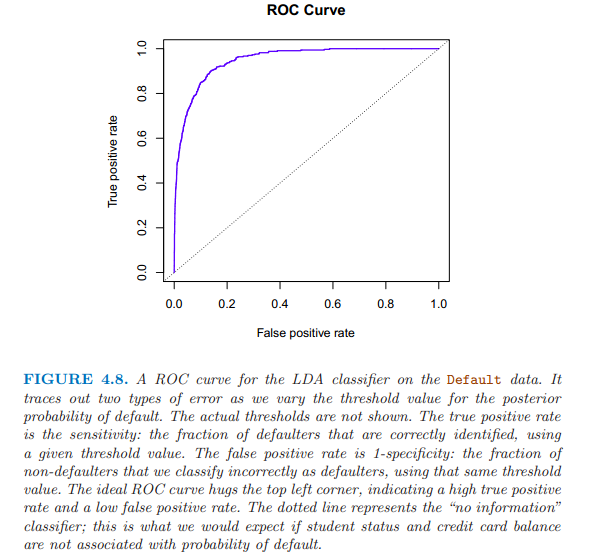
Y軸 TPR(true positive rate) sensitivity recall power 1-type 2 error:某臨界點處,被正確識別的拖欠者的比例;
X軸 FPR(false prositive rate) 1-specificity type1 error:在同一臨界點處,非拖欠者被誤判為拖欠者的比例。
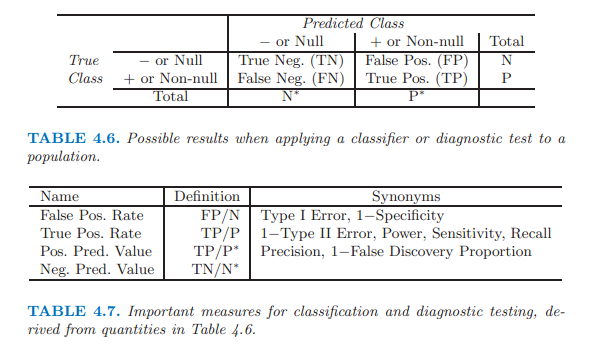
- QDA (quadratic discriminant analysis)
假定Y變量的每個類別有各自的協方差矩陣。
\[\delta_k(x) = -\frac{1}{2}(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k) + log\pi_k \\\\ = -\frac{1}{2}x^T\Sigma_k^{-1}x + x^T\Sigma_k^{-1}\mu_k - \frac{1}{2}\mu_k^T\Sigma_k^{-1}\mu_k + log\pi_k\]
選擇LDA還是QDA,基於偏差和方差之間的權衡。
如果有p個解釋變量,LDA需要估計p(p+1)/2個係數,QDA需要估計kp(p+1)/2個係數。
如果有相對少的訓練數據,使用LDA,因為降低方差是關鍵。
如果有大量的訓練數據,或者K個類別屬於共同的協方差矩陣站不住腳的時候,使用QDA。
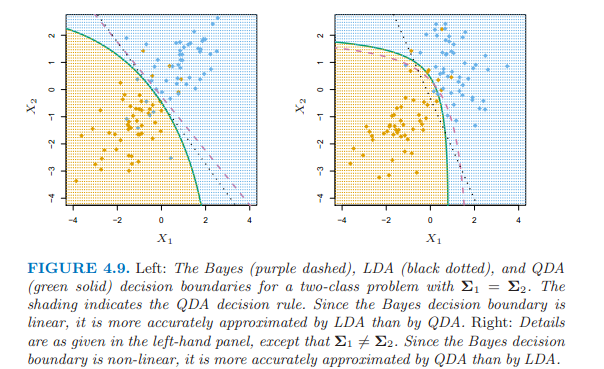
- 分類模型比較
- logistic regression
- LDA
- QDA
- KNN
logistic regression和LDA比較近似;
都產生線性決策邊界;
不同在於擬合過程不同,前者使用最大似然,後者使用正態分佈估計的均值和方差來擬合模型。
KNN是完全非參數的,適用於決策邊界高度非線性。
QDA介於上述兩者之間。
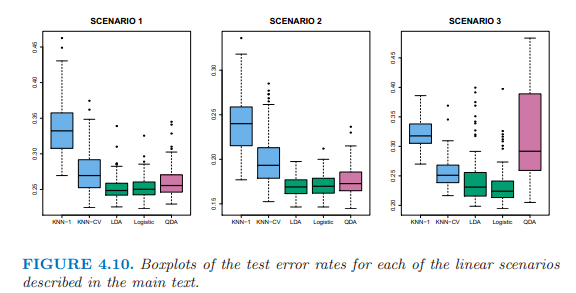
上邊的左圖:兩個解釋變量服從正態分佈,相互獨立。LDA運行的最好。
上邊的中圖:兩個解釋變量屬於正態分佈,相關係數-0.5。
上邊的右圖:兩個解釋變量服從t分佈,t分佈更偏向兩端,logistic regression 運行最好。

上邊的左圖:服從正態分佈,在第一個類別中的解釋變量之間的相關性為0.5,第二個類別間為-0.5。QDA運行最好。
上邊的中圖:正態分佈,相互獨立,使用解釋變量的平方項和交互項做解釋變量,QDA運行最好,然後是KNN-CV。
上邊的右圖:複雜的非線性,KNN-CV運行最好。
- 具體的R中的函數
logistic regression
glm(, , family = binomial) 詳見167頁
lda 詳見172頁
library(MASS)
lda()qda 詳見174頁
library(MASS)
qda()knn 詳見175頁
library(class)
knn()knn建模之前的數據需要預處理,數據標準化,統一單位,使所有變量都均值為0,標準差為1。使用scale()。
本章重點: + 邏輯回歸適用於Y有兩個類別,使用最大似然,產生線性決策邊界; + 而且,單變量邏輯回歸很危險,當單變量可能與其他變量相關時; + LDA適用於Y有三個以上類別時,使用正態分佈估計的均值和方差來擬合模型,產生線性決策邊界; + QDA,Y變量的每個類別有各自的協方差矩陣; + KNN是完全非參數的,適用於決策邊界高度非線性; + KNN建模之前的數據需要預處理,數據標準化。
备注:转移自新浪博客,截至2021年11月,原阅读数135,评论0个。