重讀《An introduction to statistical learning》筆記2 第三章
2015-03-19
chapter 3 linear regression
數學表達式 \[Y\ \approx\ \beta_{0\ }+\beta_1\cdot X\] \[Y\ =\ \beta_{0\ }+\beta_1\cdot X\ \ +\ e\] \[\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 \cdot x\]
殘差 residual
\[e_i =\ y_i -\ \hat{y}_i\]殘差平方和 RSS residual sum of squares \[RSS =\ e_1^{2} +\ e_2^{2} +\ ... +\ e_n^{2}\] \[RSS = (y_1 -\ \hat{\beta}_0 -\ \hat{\beta}_1 x_1)^{2} +\ \\\\ (y_2 -\ \hat{\beta}_0 -\ \hat{\beta}_1 x_2)^{2} +\ ... +\ \\\\ (y_n -\ \hat{\beta}_0 -\ \hat{\beta}_1 x_n)^{2} \]
使用最小平方法least square 確定使RSS最小的參數值。
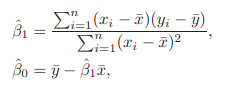
- 評估參數估計的準確性
\[Var(\hat{\mu}) =\ SE(\hat{\mu})^2 =\ \frac{\sigma^2}{n}\]
SE:standard error 標準誤,用於計算置信區間,評估估計值與真值之間的差距; 隨n即數據量增大,se減小。

\[\hat{\beta}_0 \pm 2 \cdot SE(\hat{\beta}_0)\] \[t =\ \frac{\hat{\beta}_1 - 0}{SE(\hat{\beta}_1)}\]
- 評估模型的準確性
- 殘差標準誤 RSE residual standard error
對模型的偏離的度量 a measure of the lack of fit of the model

- R square 表示Y的變動中可以用X解釋的部份的占比,也是線性關係的測量。 \[R^2 = \frac{TSS - RSS}{TSS} = 1 - \frac{RSS}{TSS}\] \[TSS = \sum(y_i - \bar{y})^2\]
- 多變量的線性回歸(書中的一個例子)
sales ~ 9.312 + 0.203*radio 顯著
sales ~ 12.351 + 0.055*newspaper 顯著
sales ~ 2.93 + 0.189radio -0.001newspaper + 0.046*tv 多變量時newspaper不顯著
cor(newspaper, radio) = 0.35
一元線性回歸中,代表報紙增加1單位后的平均效應
多元線性回歸中,代表黨tv和radio保持不變時,報紙增加1單位后的平均效益
一元模型中,報紙的顯著,因為radio增加所導致的
多元模型中,控制radio不變,就暴露出newspaper其實對sales無影響
類似于,鯊魚襲擊人類 ~ 冰激凌的銷售量,偽相關,與兩者均相關的是,天氣炎熱,氣溫高。
- 評估多變量線性模型的有效性 \[F = \frac{(TSS - RSS)/p}{RSS/(n-p-1)}\]
當F接近1時,模型失效。
F統計量適用於p(變量個數)<n(觀察值個數)
當p > n 時,不能用最小平方法擬合多變量線性回歸模型,因此,也不能用F統計量。
- 變量選擇
- 前進法(貪婪算法)
- 後退法(不適用於變量個數>觀察值個數)
- 混合法(以上兩種方法的合併,較好)
- 模型的擬合質量
主要是R square 和RSE
當添加一個無用變量時,RSE會變大
\[RSE = \sqrt{\frac{1}{n-p-1} RSS}\]
RSE類似與MSE均方誤
RSE多開了個根號
R方類似與,偏差和方差之間的權衡,可解釋誤差與不可解釋的誤差之間的比值
- 使用模型預測時的不確定性
- 參數估計的不準確 可以計算置信區間
- 模型偏差 假定為線性模型與實際的偏差
- 隨機誤差,不可縮減的誤差
- 回歸模型中的離散變量
使用一個0-1離散變量作為解釋變量
\[x_i = \begin{cases} 1 \quad if \ ith \ person\ is \ female \\\\ 0 \quad if\ ith\ person\ is \ male \end{cases}\]
\[y_i = \beta_0 + \beta_1x_i + \epsilon_i = \begin{cases} \beta_0 + \beta_1 + \epsilon_i \quad if \ ith \ person\ is \ female \\\\ \beta_0 + \epsilon_i \quad if\ ith\ person\ is \ male \end{cases}\]
參數的解釋跟以前的不同了,需要注意:
截距項代表男性信用卡的平均數;
截距項 + 斜率項 代表女性信用卡的平均數;
斜率項代表男性和女性之間的差值。
\[x_i = \begin{cases} 1 \quad if \ ith \ person\ is \ female \\\\ -1 \quad if\ ith\ person\ is \ male \end{cases}\]
\[y_i = \beta_0 + \beta_1x_i + \epsilon_i = \begin{cases} \beta_0 + \beta_1 + \epsilon_i \quad if \ ith \ person\ is \ female \\\\ \beta_0 - \beta_1 + \epsilon_i \quad if\ ith\ person\ is \ male \end{cases}\]
參數的解釋又不同了。
截距項代表總體信用卡的平均值,無視性別的影響;
斜率項代表女性高於總體水平的數值和男性低於總體水平的數值。
使用兩層以上的離散變量做解釋變量
\[x_{i1} = \begin{cases} 1 \quad if \ ith \ person\ is \ Asian \\\\ 0 \quad if\ ith\ person\ is \ not \ Asian \end{cases}\]
\[x_{i2} = \begin{cases} 1 \quad if \ ith \ person\ is \ Caucasian \\\\ 0 \quad if\ ith\ person\ is \ not \ Caucasian \end{cases}\]
\[y_i = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \epsilon_i = \begin{cases} \beta_0 + \beta_1 + \epsilon_i \quad if \ ith \ person\ is \ Asian \\\\ \beta_0 + \beta_2 + \epsilon_i \quad if \ ith \ person\ is \ Caucasian \\\\ \beta_0 + \epsilon_i \quad if\ ith\ person\ is \ African \ American \end{cases}\]
截距項代表african的信用卡數值;
斜率1代表african和asican之間的差值;
斜率2代表african和caucasian之間的差值。
- 線性模型的2個假設
additive 解釋變量之間互相獨立 \[Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \epsilon\]
如果違反了該假設,解釋變量之間互相影響,有交互項,模型為: \[Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \beta_3X_1X_2 + \epsilon\]
這裡需要注意:如果交互項顯著,組成交互項的變量不顯著,也應該包括這些不顯著的變量在模型中。
交互項不僅僅在連續變量之間,連續變量和離散變量的交互項也很有意義。
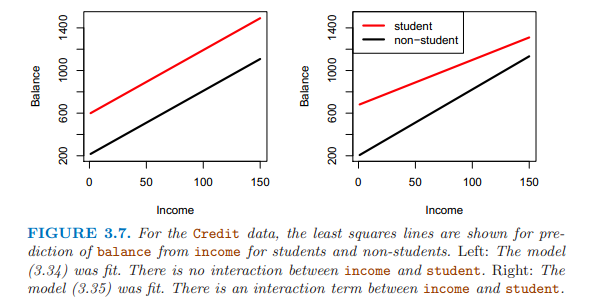
解釋變量僅有連續變量和離散變量時,模型如下所示: \[balance_i \approx\ \beta_0 + \beta_1 \times income_i + \begin{cases} \beta_2 \quad if \ ith \ person\ is \ a \ student \\\\ 0 \quad if \ ith \ person\ is \ not \ a \ student \end{cases} \\\\ = \beta_1 \times income_i + \begin{cases} \beta_0 + \beta_2 \quad if \ ith \ person\ is \ a \ student \\\\ \beta_0 \quad if \ ith \ person\ is \ not \ a \ student \end{cases}\]
兩個平行的直線,因為斜率項(連續變量的參數)相同,截距項(離散變量的取值決定是否是學生)不同;
解釋變量含有交互項時,模型如下: \[balance_i \approx\ \beta_0 + \beta_1 \times income_i + \begin{cases} \beta_2 + \beta_3 \times income_i \quad if \ student \\\\ 0 \quad if \ not \ student \end{cases} \\\\ = \beta_1 \times income_i + \begin{cases} (\beta_0 + \beta_2) + (\beta_1 + \beta_3) \times income_i \quad if \ student \\\\ \beta_0 + \beta_1 \times income_i \quad if \ not \ student \end{cases}\]
兩根直線,截距不同、斜率不同。
linear 某解釋變量改變一個單位,對預測變量的影響是個常數,即參數值。
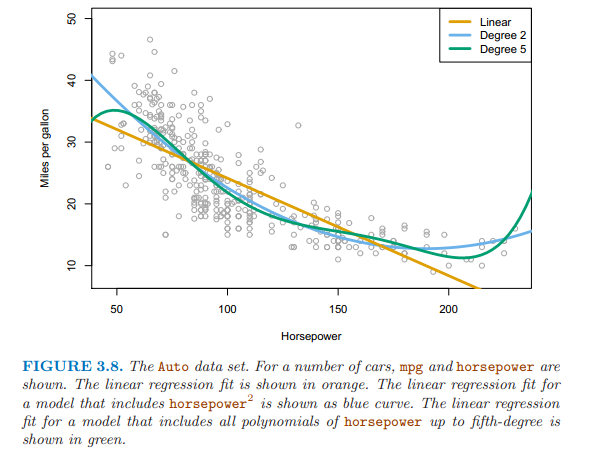
如果違反了該假設,可以使用多項式回歸,即添加解釋變量的平方項、三次方等,擬合非線性方程。
仍然是個線性模型,可以把平方項當做第二個解釋變量。 \[mpg = \beta_0 + \beta_1 \times horsepower + \beta_2 \times horsepower^2 + \epsilon\]
- 潛在的問題
- 解釋變量和響應變量之間的非線性關係
- 殘差項之間相關
- 殘差項的方差不是一個常數
- 極值
- high-leverage points
- 共線性
第一個:使用”殘差圖”確定解釋變量和響應變量之間的”非線性”關係。
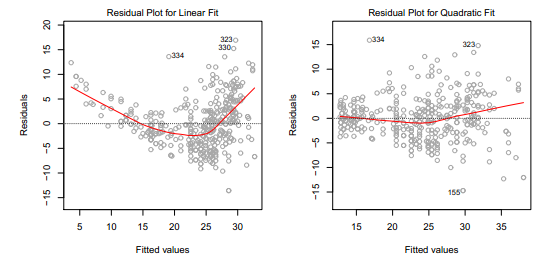
如果殘差圖中有可識別的模式,暗示了線性模型的問題。
如上面的左圖,圖中的U型暗示非線性的關係存在。
最簡單的方法是添加解釋變量的非線性的轉變,如取對數、開根號、平方。
第二個:如果殘差項之間相關,估計的標準誤會低于真實標準誤,置信區間和預測區間會變窄,模型的P值也會偏低,導致我們錯誤的推斷一個參數是顯著的。
殘差項相關通常發生在時間序列數據中,可以畫殘差圖根據時間順序, 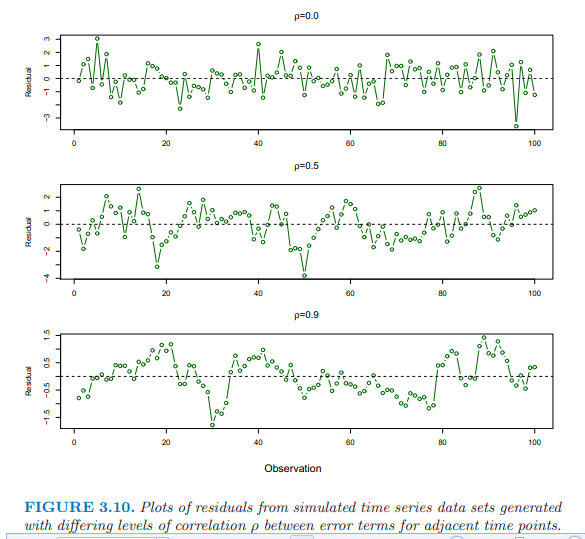
殘差項相關也會發生在其他數據中,如根據體重預測身高,一些數據來自同一個家庭中,或同樣的飲食或同樣的環境因素。
第三個:殘差項的方差不是一個常數。
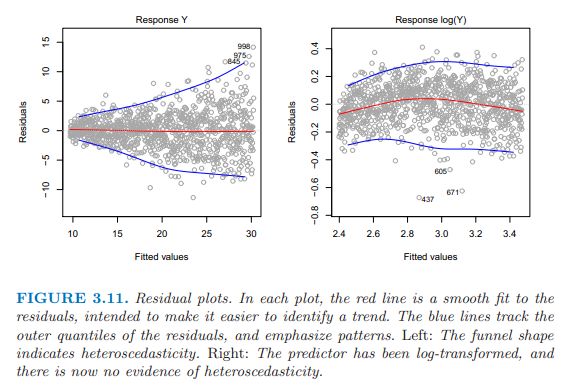
上面的左圖殘差圖就是異方差,圖形呈漏斗形。
可以對Y變量取對數或者開根號,減小異方差,如上面的右圖所示。
第四個:極值
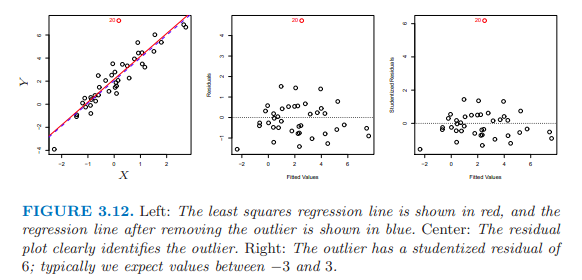
極值會影響RSE,RSE用於計算所有的置信區間和P值。
殘差圖用於發現極值點。
studentized residuals, 殘差除以估計的標準誤,其絕對值大於3,幾乎可以確定為極值點。
第五個:高杠杆點
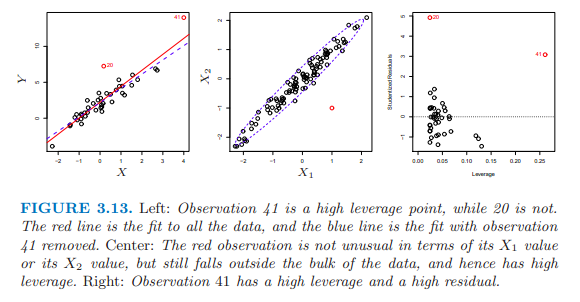
高杠杆點的移除與否對回歸線的擬合有影響,由於高杠杆點的存在,可能導致整個擬合失效。
為了確定觀察值的杠杆性,計算leverage statistic,這個值很大,意味著是個高杠杆值,平均值為(p+1)/ n。
第六點:共線性。
兩個以上的解釋變量之間高度相關。很難區別單一的共線變量對Y的影響。
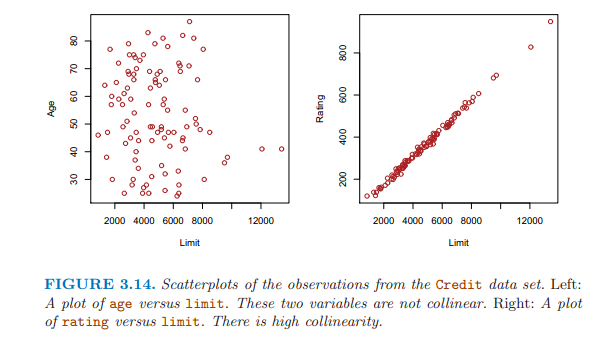
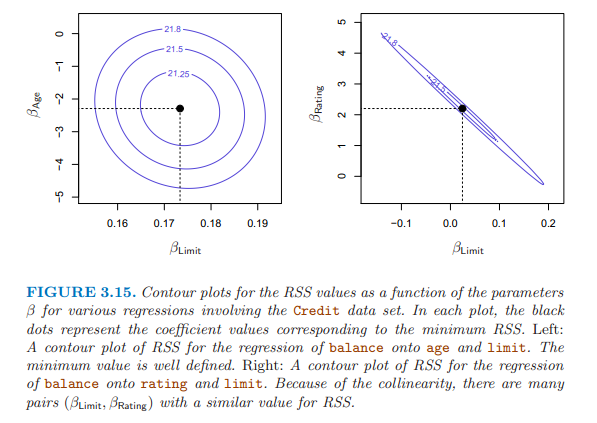
共線性降低了回歸係數估計的準確性,導致標準誤增加,拒絕參數為0 的原假設的能力降低。 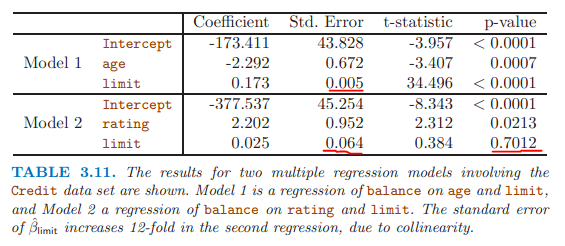
檢查解釋變量的相關矩陣發現共線性問題;
但有時共線性問題存在三個以上的變量中,為多重共線性,計算variance inflation factor (VIF),VIF大於5或者10,暗示有共線性問題。
解決:從模型中,刪除一個共線變量;把共線變量組合為一個解釋變量。
- 對比線性回歸和K個最近鄰回歸
參數方法 VS 非參數方法
給出鄰居的個數K和起始點x0,確定最接近x0的K個值,用N0表示。
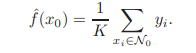
一般來說,最優值K的確定依賴于偏差和方差之間的權衡。
K值小,提供了複雜的擬合,有低偏差,高方差;這裡的高方差因為某個地方的預測僅依賴于一個觀察值。
K值大,提供了一個平滑和少變動的擬合,預測是幾個值的平均值,單個觀察值的影響小,平滑會導致偏差,因為掩蓋了模型中的某些結構。
當參數模型選擇的方程接近真實形式,參數模型優於非參模型。
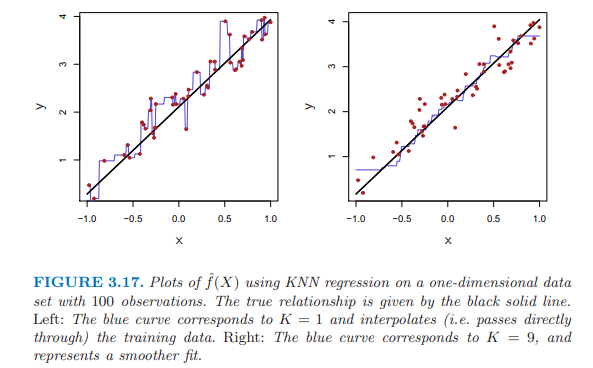
3.17兩個圖表示,K大的KNN更平滑。
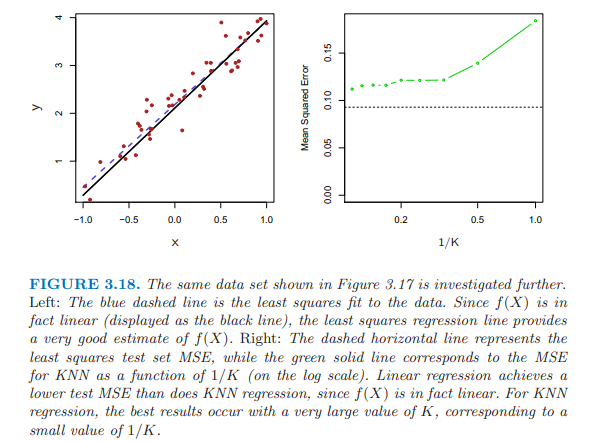
3.18圖中的真實形式是線性,線性模型優於KNN,當K很大時,表現最好,和線性模型的差距最小。
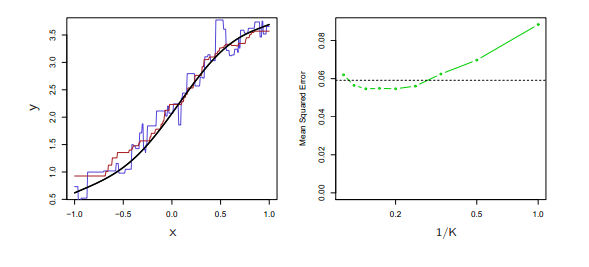
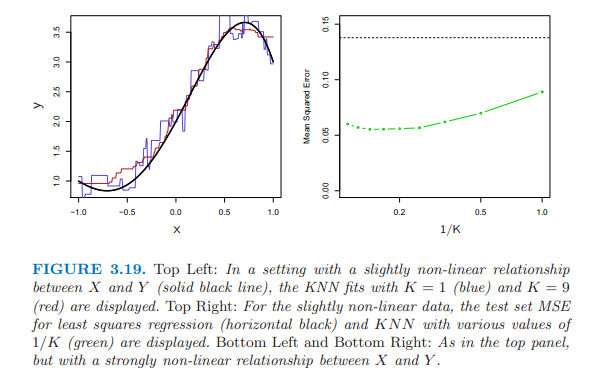
3.19上面的圖真實形式:稍微非線性,knn的擬合圖,knn與線性的MSE的比較;
3.19下面的圖真實形式:明顯非線性,KNN的擬合明顯優於線性模型。
3.18和3.19圖都是基於只有1個解釋變量,當解釋變量多時,維度增高時,KNN效果差與線性模型。
3.20 真實形式:明顯非線性,添加了一個噪音解釋變量。
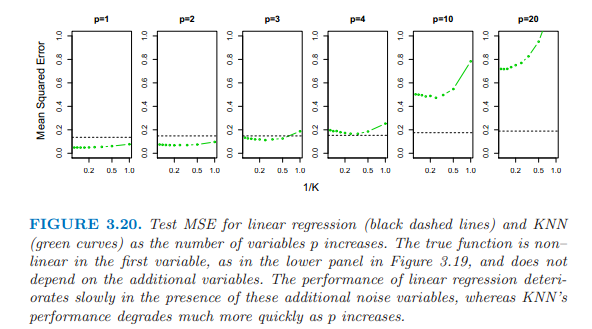
當P=1 或者P= 2 ,KNN優於線性模型;
P=3,結果是混合的;
P>= 4 線性優於KNN。
維度增加,線性模型的MSE增加了少許;
但是,KNN的MSE增加了10倍以上;
因為,維度的增加導致KNN中抽樣量的大幅減少。
如100個觀測值,1個變量,提供了足夠的信息去估計模型;
當100個觀測值,有20個變量時,一個特定的觀察值沒有鄰居,所謂的維度的詛咒(1維空間變成了20維的空間);因此KNN擬合效果很差。
一般來說,當每個解釋變量有少量觀測值時,參數方法優於非參數方法。
具體的R在線性回歸上的操作,參見原書120頁。
本章重點:
- 殘差平方和RSS、殘差標準誤RSE、R平方;
- 多元模型和一元模型的衝突,有偽相關存在;
- 使用離散變量做解釋變量時,係數的解釋;
- 違反線性回歸模型假設的識別及處理。
- 線性回歸于knn比較,線性優。
备注:转移自新浪博客,截至2021年11月,原阅读数206,评论0个。